I recently started on a quest to finish up a loose end on the AT&T 3B2 emulator by finally implementing a simulation of the WE32106 Math Acceleration Unit (MAU). The MAU is an IC that accelerates floating point operations, and it could be fitted onto the 3B2 motherboard as an optional part. I’ve seen quite a few 3B2 systems that didn’t have one; if it’s not present, the 3B2 uses software floating point emulation, and gets on just fine without it. This means the 3B2 emulator is totally usable without the MAU. But still, wouldn’t it be nice to simulate it?
Lucky for me, one of the critical pieces of documentation I’ve managed to find over the last few years is the WE32106 Math Acceleration Unit Information Manual. This little book describes the implementation details of the WE32106, and without it it would be hopeless to even try to simulate it. (Speaking of which: The book hasn’t been scanned yet, which is a high priority. I have the only copy I’ve ever seen.)
But even with the book, this is no simple task. So let’s dive in a little deeper and look under the hood of the WE32106.
Floating Point Background
The WE32106 came out in 1984, when the IEEE 754 floating point specification was just being finalized, so the chip is an extremely faithful IEEE 754 implementation. I won’t go into the nitty-gritty details of IEEE 754, because you can read about it in great detail in any number of places. But I’ll cover the basics.
Floating point numbers are stored internally in scientific notation, using the concept of an exponent and a significand (or mantissa). In decimal notation, scientific notation looks like 3.032×10-14 to represent a very small number with four significant digits. If you wrote it out in full, it would be 0.00000000000003032. That’s a lot of leading zeros. Scientific notation allows us to break the number up into an exponent (-14), and the significand or mantissa (3032). Using this format requires much less space to hold very large or very small numbers.
Of course, we don’t use decimal for storing numbers in a computer. Instead of using powers of 10, we use powers of 2. But the principal applies just the same, and we store a binary exponent and a binary mantissa (the WE32106 calls this a fraction instead of mantissa).
There are three data types used in the WE32106: Single Precision, Double Precision, and Extended Precision. The main difference between these formats is how big or small a number they can hold, and with what number of significant digits.
Single Precision numbers fit into a single 32-bit word. They use one sign bit (0 for positive, 1 for negative), 23 bits for the fraction (mantissa), and 8 bits for the exponent.
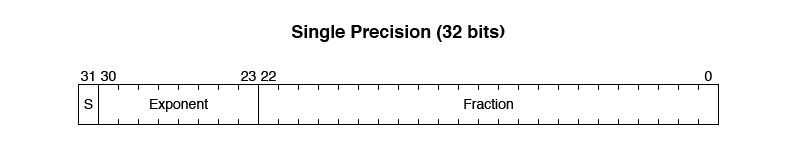
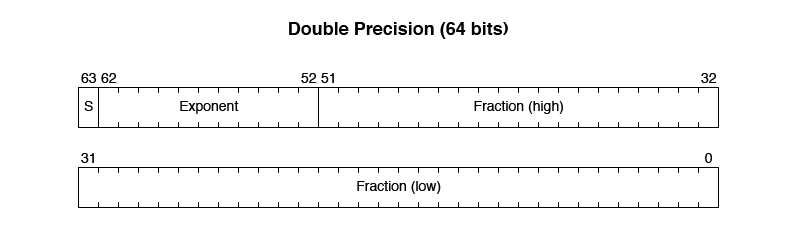
Double Precision requires 64 bits and fits into two 32-bit words. It allows for much larger and smaller values than Single Precision. It also uses one sign bit, but 52 bits for the fraction, and 11 bits for the exponent.
Finally, Extended Precision allows for holding the largest and smallest values. All of the internal registers of the WE32106 use Extended Precision. It uses 80 bits, and fits into three 32-bit words.
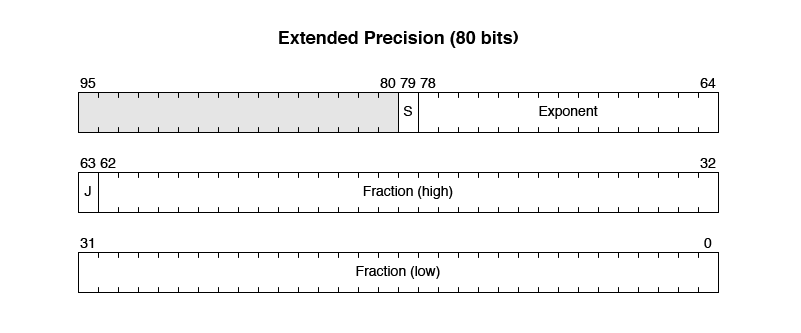
The WE32106 uses this last format for all of its internal registers and operands, so that all of its internal operations have full precision when executed. The result can be converted to a form with less precision if needed.
Simulating the WE32106
Obviously, a faithful simulation of the WE32106 needs to handle all of the operations performed by the real thing. So far this has been very slow going. The documentation I have is pretty good, but not as thorough as I would like, so I have had to resort to some trial and error. A favorite technique of mine is to run the MAU diagnostics, watch them fail, and then try to figure out what the tests were expecting and how that corresponds to what the documentation is saying. This has led to a lot of insights.
My first challenge, though, was dealing with the internal representation
of these numeric types. Here, I have cheated, and quite badly. It just so
turns out that many modern C compilers use IEEE 754 encoding under the
hood, and that many modern C compilers represent these three values with
the types float, double, and long double. Emphasis here on many.
The C standard says nothing about how numbers need to be encoded. It
certainly does not specify IEEE 754. It also doesn’t say how many bytes
each type has to be. All of that is implementation specific. But, since
the major platforms I care about all just happen to use IEEE 754 format,
I let the compiler do the work for me. Internally, I just use a C union
to access the raw bytes that represent a float, double, or long double. I store all intermediate values as long double, with a little
bit of metadata, and peform operations on long double values. Then, when
I need to write out the result somewhere, I use casts where needed and
reverse the process by writing out the correct type into another C
union.
It gets the job done. It’s also risky. I will be adding some tests that will disable the MAU immediately if certain assumptions aren’t true at runtime. Better to run without a MAU than with a MAU that has undefined behavior.
Exceptional Conditions
One of the hairier problems is how to handle all of the special values and edge cases of IEEE 754 math. I can’t just use C division to divide by zero, after all. I need to notice that the divisor is zero, and then mimic the correct exception. Otherwise, the simulator will crash. That’s no fun.
There are a lot of such edge cases, it turns out. Values can
underflow or overflow. Values can be positive zero or negative zero.
Values can be NaN. The combinatorics get hairy, and so far I’ve only
just scratched the surface in the simulation.
Where to Go From Here
I think the basic framework I’ve written so far is well on its way to being correct and usable. From here on out, I need to cover all of the special values and edge cases, do the right operations (addition, subtraction, multiplication, and division) when the values are valid, and handle potential overflows and underflows.
There’s a lot more to do, so I’ll be updating the blog here as I go.
Comments